ROTAÇÃO DA RETA
Salve, salve tripulantes dessa nave louca, estamos aqui de novo para darmos sequência ao nosso conteúdo sobre o Método Descritivo denominado Rotação, que agora, no caso, será aplicado ao Estudo da Reta.
Pois bem, a rotação da reta em torno de um eixo consiste em girar dois pontos desta em mesma amplitude e no mesmo sentido.
w = amplitude
O ideal é, sempre que possível, que a reta e o eixo devem se situar no mesmo plano, ou seja, devem ser coplanares, isto gerará uma facilidade na construção da épura, pois, um dos pontos desta reta pertencendo ao eixo de rotação, este ponto ficará imóvel, sendo bastante girar apenas um outro ponto da reta.
Tendo agora uma reta (A)(B) reversa ao eixo de rotação (e). Uma outra forma para se realizar a rotação é girar apenas o pé da perpendicular comum a reta e ao eixo:
Faz-se eB perpendicular a projeção horizontal da reta AB (neste caso do exemplo), eB = raio do círculo descrito com e sendo o centro, a PH da reta (A)(B) ficará tangente ao círculo e assim permanecerá mesmo após a rotação. Sabendo disso, basta então rotacionar o ponto B em uma determinada amplitude e pela nova projeção horizontal do deste traçar uma perpendicular em relação a eB̄, nesta perpendicular a nova projeção horizontal Ā se situará.
PRINCIPAIS APLICAÇÕES
Quando se tem uma reta qualquer e deseja-se tornar esta paralela ou perpendicular a um dos planos de projeções, podemos realizar esta ação utilizando-se das rotações. No primeiro caso, tornar paralela, basta apenas uma única rotação que chegaremos ao objetivo, já no segundo caso, tornar perpendicular, será necessário uma dupla rotação.
- Tornar frontal uma reta dada
Para tornar uma reta qualquer em uma frontal, basta realizar uma rotação em torno de um eixo vertical, de modo que após a rotação a reta dada possua as característica de uma reta frontal que é: projeção vertical obliqua a linha de terra e projeção horizontal paralela a linha de terra.
(A)(B) = Reta qualquer;
(Ā)(B̄) = Reta frontal.
- Tornar horizontal uma reta dada
Para tornar uma reta qualquer em uma horizontal, basta realizar uma rotação em torno de um eixo de topo, de modo que após a rotação a reta dada possua as característica de uma reta horizontal que é: projeção vertical paralela a linha de terra e projeção horizontal oblíqua a linha de terra.
(A)(B) = Reta qualquer;
(Ā)(B̄) = Reta horizontal.
- Tornar vertical uma reta dada
No caso de termos uma reta qualquer, cujo objetivo é torna-la vertical, serão necessárias duas rotação, uma primeira em torno de um eixo vertical de modo que esta reta qualquer dada passe a ser uma reta frontal. Na sequência faz-se agora uma rotação, nesta reta frontal, agora, em torno de um eixo de topo tornando assim essa reta que era frontal em uma reta vertical.
(A)(B) = Reta qualquer;
(Ā)(B̄) = Reta frontal;
(Ā1)(B̄1) = Reta vertical
- Tornar de topo uma reta dada
Novamente, teremos que realizar duas rotações, a primeira em torno de um eixo de topo para tornar a, então, reta qualquer em uma reta horizontal, a segunda rotação será em torno de um eixo vertical de modo que a reta horizontal torne-se uma reta de topo.
(A)(B) = Reta qualquer;
(Ā)(B̄) = Reta horizontal;
(Ā1)(B̄1) = Reta de topo
PROBLEMA FUNDAMENTAL
Girar uma reta em torno de um eixo, vertical ou de topo, até que ela se situe no plano.
Dizendo que:
Se â > b^ → 2 soluções;
Se â = b^ → 1 solução;
Se â < b^ → nenhuma solução.
Então vamos aos procedimentos:
1: leiam "jota com sinal diacrítico em cima", pois não existe esta letra alfabeto, assim não possui código html para reproduzi-la.
Pois bem, a rotação da reta em torno de um eixo consiste em girar dois pontos desta em mesma amplitude e no mesmo sentido.
O ideal é, sempre que possível, que a reta e o eixo devem se situar no mesmo plano, ou seja, devem ser coplanares, isto gerará uma facilidade na construção da épura, pois, um dos pontos desta reta pertencendo ao eixo de rotação, este ponto ficará imóvel, sendo bastante girar apenas um outro ponto da reta.
Tendo agora uma reta (A)(B) reversa ao eixo de rotação (e). Uma outra forma para se realizar a rotação é girar apenas o pé da perpendicular comum a reta e ao eixo:
Faz-se eB perpendicular a projeção horizontal da reta AB (neste caso do exemplo), eB = raio do círculo descrito com e sendo o centro, a PH da reta (A)(B) ficará tangente ao círculo e assim permanecerá mesmo após a rotação. Sabendo disso, basta então rotacionar o ponto B em uma determinada amplitude e pela nova projeção horizontal do deste traçar uma perpendicular em relação a eB̄, nesta perpendicular a nova projeção horizontal Ā se situará.
Quando se tem uma reta qualquer e deseja-se tornar esta paralela ou perpendicular a um dos planos de projeções, podemos realizar esta ação utilizando-se das rotações. No primeiro caso, tornar paralela, basta apenas uma única rotação que chegaremos ao objetivo, já no segundo caso, tornar perpendicular, será necessário uma dupla rotação.
- Tornar frontal uma reta dada
Para tornar uma reta qualquer em uma frontal, basta realizar uma rotação em torno de um eixo vertical, de modo que após a rotação a reta dada possua as característica de uma reta frontal que é: projeção vertical obliqua a linha de terra e projeção horizontal paralela a linha de terra.
(Ā)(B̄) = Reta frontal.
- Tornar horizontal uma reta dada
Para tornar uma reta qualquer em uma horizontal, basta realizar uma rotação em torno de um eixo de topo, de modo que após a rotação a reta dada possua as característica de uma reta horizontal que é: projeção vertical paralela a linha de terra e projeção horizontal oblíqua a linha de terra.
(Ā)(B̄) = Reta horizontal.
- Tornar vertical uma reta dada
No caso de termos uma reta qualquer, cujo objetivo é torna-la vertical, serão necessárias duas rotação, uma primeira em torno de um eixo vertical de modo que esta reta qualquer dada passe a ser uma reta frontal. Na sequência faz-se agora uma rotação, nesta reta frontal, agora, em torno de um eixo de topo tornando assim essa reta que era frontal em uma reta vertical.
(Ā)(B̄) = Reta frontal;
(Ā1)(B̄1) = Reta vertical
- Tornar de topo uma reta dada
Novamente, teremos que realizar duas rotações, a primeira em torno de um eixo de topo para tornar a, então, reta qualquer em uma reta horizontal, a segunda rotação será em torno de um eixo vertical de modo que a reta horizontal torne-se uma reta de topo.
(Ā)(B̄) = Reta horizontal;
(Ā1)(B̄1) = Reta de topo
Girar uma reta em torno de um eixo, vertical ou de topo, até que ela se situe no plano.
Dizendo que:
- â = ângulo da reta com o eixo
- b^ = ângulo do eixo com o plano.
Se â = b^ → 1 solução;
Se â < b^ → nenhuma solução.
Então vamos aos procedimentos:
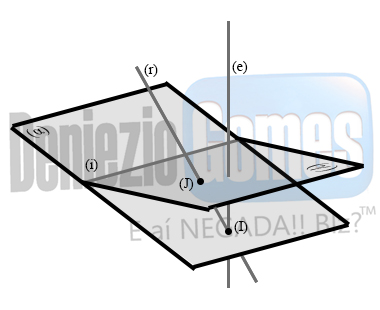
- Determina-se o traço (I) da reta sobre o plano (α);
- Por (I), faz-se passar um eixo (vertical ou de topo);
- Escolhe-se então, um ponto qualquer (J) da reta (r); - Por este ponto (J) faz-se um plano (γ) perpendicular ao eixo;
- Determina-se a reta interseção (i) entre os planos (α) e (γ);
- Situa-se o ponto (J) na reta (i), obtendo-se assim, J-1 e J-'1;
- Liga-se a projeção horizontal rotacionada do ponto (J) a projeção horizontal do ponto (I) determinando a projeção horizontal rotacionada da reta (r); - Analogamente faz-se o mesmo com a projeção vertical do ponto (J) a projeção vertical do ponto (I), determinando a projeção vertical rotacionada da reta (r).
1: leiam "jota com sinal diacrítico em cima", pois não existe esta letra alfabeto, assim não possui código html para reproduzi-la.


























0 comentários:
Postar um comentário