TRAÇOS DA RETA
Chamamos de Traços da Reta, os pontos onde a reta toca os Planos de Projeções.
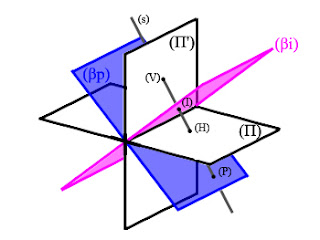
Traço Horizontal (H) da Reta.
É o ponto em que a reta atravessa o Plano Horizontal de Projeção (π), isto é, é o ponto da reta de cota nula.
Em Épura caracteriza-se por ter a Projeção Vertical na Linha de Terra (ππ').
- Determinação do Traço Horizontal (H) da Reta.
Para determinar o Traço Horizontal (H) da reta, em Épura, basta prolongar a projeção vertical da reta até a Linha de Terra (ππ'), o ponto onde a projeção vertical tocar a Linha de Terra (ππ'), encontramos a projeção vertical H' do traço horizontal (H), a seguir, basta traçar uma linha de chamada perpendicular a Linha de Terra (ππ') até a projeção horizontal da reta, onde a linha de chamada tocar a projeção horizontal da reta, encontra-se a projeção horizontal H do traço horizontal (H) da reta.
Traço Vertical (V) da Reta.
É o ponto em que a reta atravessa o Plano Vertical de Projeção (π'), isto é, é o ponto da reta de afastamento nulo.
Em Épura caracteriza-se por ter a Projeção Horizontal na Linha de Terra (ππ').
- Determinação do Traço Vertical (V) da Reta.
Para determinar o Traço Vertical (V) da reta, basta prolongar a projeção horizontal da reta até a Linha de Terra (ππ'), o ponto onde a projeção horizontal da reta tocar a Linha de Terra (ππ'), encontramos a projeção horizontal V do Traço Vertical (V), na sequência basta traçar uma linha de chamada perpendicular a Linha de Terra (ππ') até a projeção vertical da reta, onde a linha de chamada tocar a projeção vertical da reta, encontra-se a projeção vertical V' do Traço Vertical (V).
01 - Determinar o traço horizontal (H) e o traço vertical (V) das retas (A)(B) e (C)(D), sendo:
(A){3; 2; -1}, (B){6; 3; 1} e (C){7; 0,5; 2}, (D){10; -6; 1}.
02 - Construir as projeções ortogonais e determinar os traços da reta (A)(B), sabendo-se que ela passa pelo 2º diedro, sendo:
(A){3; 6; 2}, (B){9; ?; ?} e (H){6; -2; ?} o traço horizontal da reta.
03 - Dada a reta (A){0; -2; -1} (B){4; 2; 2,5;}, pede-se:
a) Sua épura;
b) Seus traços;
c) Os diedros que ela atravessa;
d) Sua posição no espaço.
Veja a lista de exercício completa: Clicando Aqui.
Acesse o Canal DeniezioGomezII no Youtube para mais videoaulas.
Para fazer o Download da nossa apostila: >>> CLIQUE AQUI <<<



























0 comentários:
Postar um comentário