ROTAÇÃO DO PONTO
Em torno de um Eixo Vertical
Quando um ponto é rotacionado em torno de um eixo vertical, o círculo por ele descrito pertence a um plano horizontal.
A projeção horizontal do ponto realiza em torno do traço horizontal do eixo uma rotação de mesma amplitude e de mesmo raio.
(A)(O)(Ā) = W = AOĀ
(A)(O) = AO = raio
A cota do ponto permanece constante durante e após a rotação, qualquer que seja a amplitude (W) da rotação.
(A)A = (Ā)Ā = z(A)
Exemplo 01 - Através de uma rotação em torno de um eixo (e), situar o ponto (A) no (βi).
Exemplo 02 - Efetuar a rotação do ponto (A) em torno de um eixo (O)(Z) até situá-lo no plano vertical de projeção (π). Dados: (A){0; -1; -3}, (Z){-3; -2; -5} e (O){?; ?; 0}.
Em torno de um Eixo de Topo
Quando um ponto é rotacionado em torno de um eixo de topo, o círculo por ele descrito pertence a um plano frontal.
A projeção vertical do ponto realiza em torno do traço vertical do eixo uma rotação de mesma amplitude e mesmo raio.
(A)(O)(Ā) = W = A'OĀ'
(A)(O) = A'O = raio
O afastamento do ponto permanece constante durante e após a rotação, qualquer que seja a amplitude (W) da rotação.
(A)A' = (Ā)Ā' = y(A)
Exemplo - Através de uma rotação em torno de um eixo (Z)(O), situar o ponto (A) no (βp).
Em torno de um Eixo Horizontal
Quando o eixo dado é uma Reta Horizontal, reta esta que não é perpendicular a nenhum plano de projeção, é necessário inicialmente a realização de uma Mudança de Plano Vertical de modo a torna-la perpendicular a esse plano. Assim, a Reta Horizontal após a MPV passa a ser uma Reta de Topo. Na sequência procede-se a Rotação conforme explicado no tópico: Rotação em torno de Eixo de Topo.
Em torno de um Eixo Frontal
Quando o eixo dado é uma Reta Frontal, reta esta que não é perpendicular a nenhum plano de projeção, é necessário inicialmente a realização de uma Mudança de Plano Horizontal de modo a torna-la perpendicular a esse plano. Assim, a Reta Frontal após a MPH passa a ser uma Reta Vertical. Na sequência procede-se a Rotação conforme explicado no tópico: Rotação em torno de um Eixo Vertical.
Rotação em torno de um Eixo Fronto-Horizontal
Nesse caso, pelo fato da reta usada como eixo ser paralela a ambos os planos de projeções, é necessário a realização de uma MPV ou MPH, de modo que a reta fronto-horizontal torne-se uma reta de topo ou uma reta vertical, respectivamente. E assim procede-se a rotação conforme o caso.
MPV
MPH
Porém, neste caso, além das soluções descritas ainda pode-se, pelo fato do plano gerado ao deslocar-se o ponto em torno da reta fronto-horizontal ser de Perfil, determinar as projeções laterais do centro de rotação e do ponto ao qual deseja-se rotacionar. Com isso teremos o raio da rotação em verdadeira grandeza no Plano Lateral de Projeção, assim, basta realizar a rotação no plano lateral e na sequência determinar as projeções horizontal e vertical do ponto rotacionado.
Em torno de um eixo qualquer
Quando dispomos de um eixo qualquer (reta qualquer) e objetivamos realizar a rotação de um ponto em torno deste, podemos chegar a solução aplicando uma dupla mudança de planos. A primeira mudança tornará este eixo qualquer paralelo a um dos planos de projeções, a segunda mudança tornará o eixo perpendicular ao outro plano de plano.
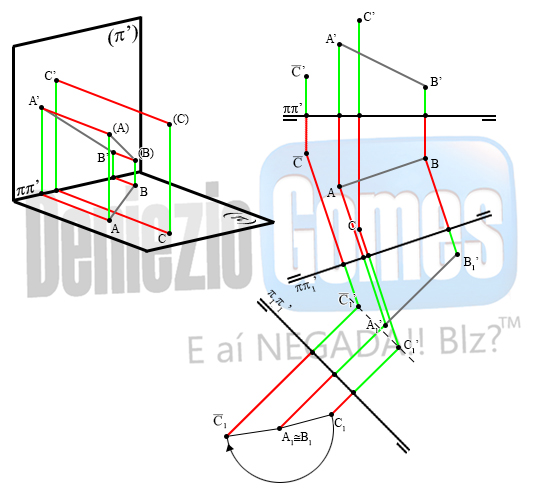
No exemplo abaixo, temos um eixo qualquer (A)(B) e queremos rotacionar o ponto (C) em torno deste. Assim, para a solução, foi realizada inicialmente uma MPH tornando o eixo (A)(B) que era um eixo qualquer em um eixo horizontal, isso ocorreu devido a linha de terra do segundo sistema foi construída paralelamente a PV do eixo (A)(B).
Na sequencia foi realizado então uma MPV tornando o eixo horizontal em um eixo de topo, essa mudança ocorre construindo-se a a linha de terra do terceiro sistema perpendicular a projeção horizontal do eixo horizontal (A)(B).
Por fim, procedeu-se a rotação no terceiro sistema e transportou-se as projeções do ponto rotacionado do 3º para o 1º sistema.
Analogamente, agora iniciando-se com uma MPV. Na figura abaixo, foi realizada inicialmente uma MPV tornando o eixo (A)(B) que era um eixo qualquer em um eixo frontal, isso ocorreu devido a linha de terra do segundo sistema foi construída paralelamente a PH do eixo (A)(B).
Na sequencia foi realizado então uma MPH tornando o eixo frontal em um eixo vertical, essa mudança ocorre construindo-se a linha de terra do terceiro sistema perpendicular a projeção vertical do eixo horizontal (A)(B).
Por fim, procedeu-se a rotação no terceiro sistema e transportou-se as projeções do ponto rotacionado do 3º para o 1º sistema.
Em torno de um eixo de perfil
[...]
Problemas Fundamentais
Sendo dados um ponto, uma reta e um plano. Pede-se: Girar o ponto em torno da reta até situá-lo no plano.
Quando um ponto é rotacionado em torno de um eixo vertical, o círculo por ele descrito pertence a um plano horizontal.
A projeção horizontal do ponto realiza em torno do traço horizontal do eixo uma rotação de mesma amplitude e de mesmo raio.
(A)(O) = AO = raio
A cota do ponto permanece constante durante e após a rotação, qualquer que seja a amplitude (W) da rotação.
Exemplo 01 - Através de uma rotação em torno de um eixo (e), situar o ponto (A) no (βi).
Exemplo 02 - Efetuar a rotação do ponto (A) em torno de um eixo (O)(Z) até situá-lo no plano vertical de projeção (π). Dados: (A){0; -1; -3}, (Z){-3; -2; -5} e (O){?; ?; 0}.
Em torno de um Eixo de Topo
Quando um ponto é rotacionado em torno de um eixo de topo, o círculo por ele descrito pertence a um plano frontal.
A projeção vertical do ponto realiza em torno do traço vertical do eixo uma rotação de mesma amplitude e mesmo raio.
(A)(O) = A'O = raio
O afastamento do ponto permanece constante durante e após a rotação, qualquer que seja a amplitude (W) da rotação.
Exemplo - Através de uma rotação em torno de um eixo (Z)(O), situar o ponto (A) no (βp).
Em torno de um Eixo Horizontal
Quando o eixo dado é uma Reta Horizontal, reta esta que não é perpendicular a nenhum plano de projeção, é necessário inicialmente a realização de uma Mudança de Plano Vertical de modo a torna-la perpendicular a esse plano. Assim, a Reta Horizontal após a MPV passa a ser uma Reta de Topo. Na sequência procede-se a Rotação conforme explicado no tópico: Rotação em torno de Eixo de Topo.
Em torno de um Eixo Frontal
Quando o eixo dado é uma Reta Frontal, reta esta que não é perpendicular a nenhum plano de projeção, é necessário inicialmente a realização de uma Mudança de Plano Horizontal de modo a torna-la perpendicular a esse plano. Assim, a Reta Frontal após a MPH passa a ser uma Reta Vertical. Na sequência procede-se a Rotação conforme explicado no tópico: Rotação em torno de um Eixo Vertical.
Rotação em torno de um Eixo Fronto-Horizontal
Nesse caso, pelo fato da reta usada como eixo ser paralela a ambos os planos de projeções, é necessário a realização de uma MPV ou MPH, de modo que a reta fronto-horizontal torne-se uma reta de topo ou uma reta vertical, respectivamente. E assim procede-se a rotação conforme o caso.
Porém, neste caso, além das soluções descritas ainda pode-se, pelo fato do plano gerado ao deslocar-se o ponto em torno da reta fronto-horizontal ser de Perfil, determinar as projeções laterais do centro de rotação e do ponto ao qual deseja-se rotacionar. Com isso teremos o raio da rotação em verdadeira grandeza no Plano Lateral de Projeção, assim, basta realizar a rotação no plano lateral e na sequência determinar as projeções horizontal e vertical do ponto rotacionado.
Em torno de um eixo qualquer
Quando dispomos de um eixo qualquer (reta qualquer) e objetivamos realizar a rotação de um ponto em torno deste, podemos chegar a solução aplicando uma dupla mudança de planos. A primeira mudança tornará este eixo qualquer paralelo a um dos planos de projeções, a segunda mudança tornará o eixo perpendicular ao outro plano de plano.
No exemplo abaixo, temos um eixo qualquer (A)(B) e queremos rotacionar o ponto (C) em torno deste. Assim, para a solução, foi realizada inicialmente uma MPH tornando o eixo (A)(B) que era um eixo qualquer em um eixo horizontal, isso ocorreu devido a linha de terra do segundo sistema foi construída paralelamente a PV do eixo (A)(B).
Na sequencia foi realizado então uma MPV tornando o eixo horizontal em um eixo de topo, essa mudança ocorre construindo-se a a linha de terra do terceiro sistema perpendicular a projeção horizontal do eixo horizontal (A)(B).
Por fim, procedeu-se a rotação no terceiro sistema e transportou-se as projeções do ponto rotacionado do 3º para o 1º sistema.
Analogamente, agora iniciando-se com uma MPV. Na figura abaixo, foi realizada inicialmente uma MPV tornando o eixo (A)(B) que era um eixo qualquer em um eixo frontal, isso ocorreu devido a linha de terra do segundo sistema foi construída paralelamente a PH do eixo (A)(B).
Na sequencia foi realizado então uma MPH tornando o eixo frontal em um eixo vertical, essa mudança ocorre construindo-se a linha de terra do terceiro sistema perpendicular a projeção vertical do eixo horizontal (A)(B).
Por fim, procedeu-se a rotação no terceiro sistema e transportou-se as projeções do ponto rotacionado do 3º para o 1º sistema.
Em torno de um eixo de perfil
[...]
Sendo dados um ponto, uma reta e um plano. Pede-se: Girar o ponto em torno da reta até situá-lo no plano.
- No primeiro caso temos que a distância do eixo ao plano menor que o raio, assim, temos duas possíveis soluções;
- No segundo caso temos que a distância do eixo ao plano igual ao raio, assim, temos uma única solução;
- Por fim no terceiro caso, temos que a distância do eixo ao plano maior que o raio, nessa situação não temos solução.






























0 comentários:
Postar um comentário