Então pessoas, tudo beleza?
Vamos dar sequência ao nosso minicurso de Excel aplicado a Topografia, mais precisamente em como realizar um cálculo de uma poligonal fechada com essa ferramenta. O interessante é que, com os conhecimentos adquiridos neste minicurso, vocês facilmente poderão aplicar em outros métodos topográficos o que aprenderem aqui.
Para hoje, vamos iniciar a nossa Planilha de Cálculos com a determinação do Erro Angular, da Correção Angular e por fim os Ângulos Horizontais Corrigidos.
Pois bem, vamos ao que interessa.
De início, abram a nossa pasta de trabalho no Excel, que deve estar assim:
Agora com nossa planilha aberta, tem-se duas opções: 1 - Continuar nessa planilha e dar sequência aos cálculos, ou, 2 - Criar uma nova planilha dentro dessa pasta de trabalho.
Pessoalmente eu prefiro criar uma nova planilha, e assim eu o farei. E esta nova planilha chamarei de Planilha_de_Calculo. E para isso basta clicar nesse símbolo de + ao lado da aba em que se encontra a planilha da Caderneta_de_Campo.
Aqueles que preferirem continuar na mesma planilha pulem esta etapa e vão onde realmente começamos a trabalhar.
Fazendo isso, basta então inserir o nome da nova planilha clicando duas vezes sobre o nome plan1. Ao final a planilha de vocês deve se encontrar assim.
Agora sim, vamos começar a trabalhar (aqueles que pularam começam aqui) nossa planilha de cálculos.
Para iniciar vamos reescrever os dados que realmente iremos utilizar da Caderneta de Campo para nossa Planilha de Cálculos, no caso vamos copiar as colunas A, B e C da Caderneta_de_Campo e colar na Planilha_de_Calculos.
Como também iremos copiar as colunas P, Q, R e S da Caderneta_de_Campo e colar na Planilha_de_Calculos.
Percebam que ao fazer isto, o resultado das células ficaram com vários erros. Isso se deve ao fato de termos fórmulas declaradas nas colunas P, Q, R e S, e na nova planilha essas fórmulas estão endereçadas para dados que não existem nela. Mas, sem esquentar a cabeça facilmente resolvemos este problema.
Basta ir na Célula G4 que está mesclada com a G5 (Planilha_de_Calculos), e digitar =, na sequência, vamos na Caderneta_de_Campo e clicamos sobre a Célula S4 que está mesclada com a célula S5, por fim pressionamos enter.
Ao darmos enter, o ângulo horizontal correto em grau decimal aparece na célula G4/G5, como também em arco sexagesimal, já que nestas células o endereçamento dessas células são para a célula do grau decimal.
Para as demais células dessa coluna, basta selecionar a primeira e arrastar para baixo, que teremos um auto preenchimento.
Pronto. Agora vamos iniciar realmente os cálculos de nossa planilha.
Como inicialmente iremos trabalhar com os dados angulares de nossa poligonal, os dados lineares (distâncias) serão copiados para a planilha de cálculos posteriormente.
Para quem me acompanha aqui no blogger ou no YouTube, já tem o conhecimento de que em uma poligonal geometricamente fechada (Ea = 0), a soma dos ângulos, no sistema sexagesimal, obedece a uma das seguintes fórmulas:
Σai = 180° * (n-2) → Para ângulos internos a poligonal.
Σae = 180° * (n+2) → Para ângulos externos a poligonal.
Em que: n = nº de vértices da poligonal.
A não ser que vocês acochambrem umas paradas, é evidente que o somatório dos ângulos medidos em campo vai discrepar do resultado do somatório dado por umas das fórmulas acima. Essa diferença é o que chamamos de Erro Angular.
Assim, o erro angular é dado:
Ea = Sa - Σa
Em que:
Sa = somatório dos ângulos medidos em campo;
Σa = somatório angular de uma poligonal geométricamente fechada.
Sabendo disso, vamos jogar essas fórmulas em nossa Planilha.
Para o Sa usaremos a Função SOMA do Excel, onde, basta na célula onde queremos identificar esse valor digitar =SOMA(Selecionar as células que deseja fazer a soma)
Nota: clicamos na primeira célula, pressionamos SHIFT e clicamos na última célula.
E por fim pressionamos enter.
Agora por estética, vamos preencher as colunas D, E e F da linha 17, no caso inserirmos as fórmulas de conversão de Grau Decimal para arco sexagesimal. Para isso, vamo apenas copiar da Caderneta_de_Campo e colar na Planilha_de_Cálculo.
Para o Σa vamos apenas replicar a fórmula no Excel, só temos que atentar ao seguinte, neste, precisamos do número de vértices. Aí fica a seu critério, digitar logo o valor, ou declarar n em uma célula, para automatizar a parada eu vou na segunda opção.
Para isso, vamos utilizar a Função CONT.valores, essa função conta o número de células não vazias, assim, usando ela e selecionando as células das estações, que são iguais ao números de vértices, ela chegará ao número de vértices de nossa poligonal, após pressionar ENTER.
Agora vamos aplicar a fórmula do somatório dos ângulos de uma poligonal geométricamente fechada, lembrando que para nosso caso os angulos medidos foram externos a poligonal como citado no post anterior. Assim:
Σae = 180° * (n+2)
No Excel:
Desta forma, já temos o Sa e o Σa podemos calcular o Erro Ângular (Ea).
Com isso calculamos o Erro Angular cometido em nosso levantamento. Destaco aqui, que após a determinação do Erro Angular, precisamos verificar a Tolerância Angular para o Levantamento, ou seja, o que é tolerável errar angularmente. Esta tolerância, depende do número de vértices e da precisão angular do equipamento utilizado no levantamento, para mais informações sobre tolerância angular recomendo que leiam a NBR 13133, ou essa postagem AQUI, de nosso blog. Pois, para essa poligonal sei que a mesma está dentro da tolerância e não é objetivo dessas postagens a explicação sobre a Tolerância Angular. Cabe ressaltar que, levantamentos fora da Tolerância Angular devem a via de fato e dúvidas serem refeitos por completo, ou, para profissionais que dominam o Ajustamento das Observações a aplicação de Testes para determinar se houveram erros em um ou mais vértices para retornar a campo e realizar novamente as medidas apenas nos vértices que apresentaram erros, como por exemplo, com o Teste de Baarda.
Vamos então para a Correção Angular.
O erro angular é distribuído equitativamente para todos os vértices da poligonal. A correção ângular deve ser em sinal contrário do erro angular. Assim a Correção Angular é expressa:
Ca = -(Ea/n)
Em que:
n = nº de vértices da poligonal.
No Excel:
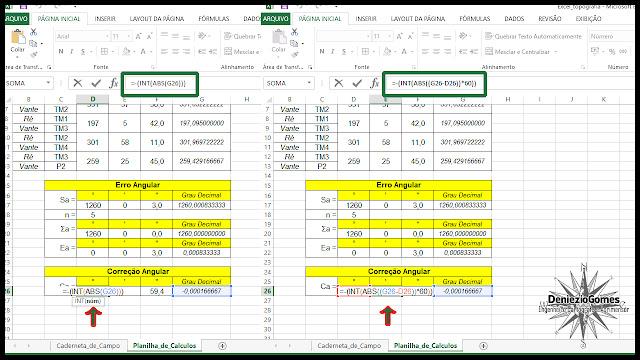
Agora, ao tentar fazer a "estética" de nossa planilha chegaremos a um, bug, valor bem louco...
Isso ocorre pelo fato da nossa equação de transformação de Grau Decimal para Arco Sexagesimal só trabalhar com valores positivos, como a correção angular foi negativa esse bug aconteceu, mas, relaxem que é bem simples de ser resolvido.
Vamos utilizar a Função ABS, que retorna o valor absoluto de um número expresso na célula. Como também vamos realizar uma adaptação. Nota: Esse desenvolvimento foi eu que fiz, não vi em nenhum lugar essa metodologia, em resumo: Sou foda!!.
Sabemos que:
Para o valor do Grau usamos: INT(Grau Decimal);
Para o valor dos Minutos usamos: INT((Grau Decimal - INT(Grau Decimal))*60); e
Para o valor dos Segundos usamos: ((Grau Decimal - INT(Grau Decimal)*60 - INT((Grau Decimal - INT(Grau Decimal))*60))*60
Para trabalhar com valores negativos temos que adaptar, no caso:
Para o valor do Grau usamos: -(INT(ABS(Grau Decimal)));
Para o valor dos Minutos usamos: -(INT((ABS(Grau Decimal) - (INT(ABS(Grau Decimal))))*60)); e
Para o valor dos Segundos usamos: ((Grau Decimal - INT(Grau Decimal)*60 - INT((Grau Decimal - INT(Grau Decimal))*60))*60. Isso mesmo, para o cálculo dos segundos, não tem alteração na fórmula.
Percebam, em todos os valores eu informei para calcular o valor absoluto (módulo), ou seja, positivo da célula selecionada, e então com toda a fórmula fechada entre parênteses inseri o valor negativo para que o resultado fosse dado de acordo com o valor real.
Aplicando essa parada toda no Excel (para o grau e minuto), é bem simples, pois só iremos alterar o que já temos, vejamos:
Pressionando ENTER, o resultado será mostrado conforme.
Pronto, agora vamos ao próximo passo para finalizar esta etapa de nossa planilha e esta postagem.
A os ângulos horizontais corrigidos são feitos de forma direta, pois, como temos o valor da correção angular por vértice basta somar esta a cada ângulo medido no levantamento.
α = αcampo + Ca
Voltando ao Excel, vamos então inserir as quatro colunas referentes aos ângulos horizontais corrigidos (Grau, Minuto, Segundo e Grau Decimal).
Então agora vamos inserir a equação para calcular cada ângulo horizontal corrigido.
Já esteticamente formatada essa linha.
Agora para completar as demais células referentes aos ângulos horizontais corrigidos, não podemos apenas arrastar para baixo a fórmula declarada em K4, isso se deve ao fato do Excel entender que ao arrastar uma fórmula de uma célula de cima para uma de baixo, os valores ao qual ele irá buscar também irão descer, por exemplo:
Vejam que ao arrastarmos apenas uma célula para baixo, o Excel entendeu que, o ângulo também desceria uma célula e como as células dos ângulos horizontais e ângulos horizontais corrigidos, são iguais, no caso, tem a mesma configuração, ou seja, são um mesclado de duas linhas e estão na mesma posição, corretamente a fórmula declarada ao descer foi buscar o valor na célula correta, enquanto que a correção angular, por não ser configurada igual a célula do ângulo horizontal corrigido, desceu duas linhas, indo então para uma célula que estava vazia, causando um erro no cálculo.
E aí, como resolvemos isso?... Bem simples pessoas, como nessa situação, a correção angular é a mesma para todos os ângulos horizontais, vamos fixar a célula da correção angular na declaração da fórmula.
E como fixamos uma célula em uma equação do Excel?... Inserindo o símbolo $ antes da referência da coluna e $ antes da referência da linha.
No caso de nossa planilha, a correção angular encontra-se na célula G26, assim, para fixarmos ela na declaração da fórmula do ângulo horizontal corrigido, fazemos: $G$26.
Simples, não!
Fazendo isso o Excel vai entender que só irá mudar o ângulo, porém a correção será a mesma para todos os ângulos, então agora basta clicar na célula que acabamos de declarar a fórmula e então arrastar para baixo.
Pronto, para finalizar vamos arrastar as fórmulas para a conversão em arcos sexagesimais.
Com isso, esta etapa dos cálculos é finalizada. Agora em nossa Planilha de Cálculos, temos: O Erro angular, a Correção angular e os Ângulos horizontais corrigidos.
Então galera, espero que vocês tenham conseguido acompanhar e chegado até aqui junto comigo. Na próxima postagem, vamos realizar o cálculo dos Azimutes dos Alinhamentos.
Vamos dar sequência ao nosso minicurso de Excel aplicado a Topografia, mais precisamente em como realizar um cálculo de uma poligonal fechada com essa ferramenta. O interessante é que, com os conhecimentos adquiridos neste minicurso, vocês facilmente poderão aplicar em outros métodos topográficos o que aprenderem aqui.
Para hoje, vamos iniciar a nossa Planilha de Cálculos com a determinação do Erro Angular, da Correção Angular e por fim os Ângulos Horizontais Corrigidos.
Pois bem, vamos ao que interessa.
De início, abram a nossa pasta de trabalho no Excel, que deve estar assim:
Agora com nossa planilha aberta, tem-se duas opções: 1 - Continuar nessa planilha e dar sequência aos cálculos, ou, 2 - Criar uma nova planilha dentro dessa pasta de trabalho.
Pessoalmente eu prefiro criar uma nova planilha, e assim eu o farei. E esta nova planilha chamarei de Planilha_de_Calculo. E para isso basta clicar nesse símbolo de + ao lado da aba em que se encontra a planilha da Caderneta_de_Campo.
Fazendo isso, basta então inserir o nome da nova planilha clicando duas vezes sobre o nome plan1. Ao final a planilha de vocês deve se encontrar assim.
OBS: Eu não coloquei acento agudo por analfabetismo funcional não galera, o motivo é que não é recomendado inserir caracteres especiais em nomes de arquivos de determinados softwares e as planilhas eletrônicas estão nessa lista.
Agora sim, vamos começar a trabalhar (aqueles que pularam começam aqui) nossa planilha de cálculos.
Para iniciar vamos reescrever os dados que realmente iremos utilizar da Caderneta de Campo para nossa Planilha de Cálculos, no caso vamos copiar as colunas A, B e C da Caderneta_de_Campo e colar na Planilha_de_Calculos.
Como também iremos copiar as colunas P, Q, R e S da Caderneta_de_Campo e colar na Planilha_de_Calculos.
Percebam que ao fazer isto, o resultado das células ficaram com vários erros. Isso se deve ao fato de termos fórmulas declaradas nas colunas P, Q, R e S, e na nova planilha essas fórmulas estão endereçadas para dados que não existem nela. Mas, sem esquentar a cabeça facilmente resolvemos este problema.
Basta ir na Célula G4 que está mesclada com a G5 (Planilha_de_Calculos), e digitar =, na sequência, vamos na Caderneta_de_Campo e clicamos sobre a Célula S4 que está mesclada com a célula S5, por fim pressionamos enter.
Ao darmos enter, o ângulo horizontal correto em grau decimal aparece na célula G4/G5, como também em arco sexagesimal, já que nestas células o endereçamento dessas células são para a célula do grau decimal.
Para as demais células dessa coluna, basta selecionar a primeira e arrastar para baixo, que teremos um auto preenchimento.
Pronto. Agora vamos iniciar realmente os cálculos de nossa planilha.
Erro Angular Ea
Para quem me acompanha aqui no blogger ou no YouTube, já tem o conhecimento de que em uma poligonal geometricamente fechada (Ea = 0), a soma dos ângulos, no sistema sexagesimal, obedece a uma das seguintes fórmulas:
Σai = 180° * (n-2) → Para ângulos internos a poligonal.
Σae = 180° * (n+2) → Para ângulos externos a poligonal.
Em que: n = nº de vértices da poligonal.
A não ser que vocês acochambrem umas paradas, é evidente que o somatório dos ângulos medidos em campo vai discrepar do resultado do somatório dado por umas das fórmulas acima. Essa diferença é o que chamamos de Erro Angular.
Assim, o erro angular é dado:
Em que:
Sa = somatório dos ângulos medidos em campo;
Σa = somatório angular de uma poligonal geométricamente fechada.
Sabendo disso, vamos jogar essas fórmulas em nossa Planilha.
Para o Sa usaremos a Função SOMA do Excel, onde, basta na célula onde queremos identificar esse valor digitar =SOMA(Selecionar as células que deseja fazer a soma)
Nota: clicamos na primeira célula, pressionamos SHIFT e clicamos na última célula.
E por fim pressionamos enter.
Agora por estética, vamos preencher as colunas D, E e F da linha 17, no caso inserirmos as fórmulas de conversão de Grau Decimal para arco sexagesimal. Para isso, vamo apenas copiar da Caderneta_de_Campo e colar na Planilha_de_Cálculo.
Para o Σa vamos apenas replicar a fórmula no Excel, só temos que atentar ao seguinte, neste, precisamos do número de vértices. Aí fica a seu critério, digitar logo o valor, ou declarar n em uma célula, para automatizar a parada eu vou na segunda opção.
Para isso, vamos utilizar a Função CONT.valores, essa função conta o número de células não vazias, assim, usando ela e selecionando as células das estações, que são iguais ao números de vértices, ela chegará ao número de vértices de nossa poligonal, após pressionar ENTER.
Agora vamos aplicar a fórmula do somatório dos ângulos de uma poligonal geométricamente fechada, lembrando que para nosso caso os angulos medidos foram externos a poligonal como citado no post anterior. Assim:
No Excel:
Desta forma, já temos o Sa e o Σa podemos calcular o Erro Ângular (Ea).
Com isso calculamos o Erro Angular cometido em nosso levantamento. Destaco aqui, que após a determinação do Erro Angular, precisamos verificar a Tolerância Angular para o Levantamento, ou seja, o que é tolerável errar angularmente. Esta tolerância, depende do número de vértices e da precisão angular do equipamento utilizado no levantamento, para mais informações sobre tolerância angular recomendo que leiam a NBR 13133, ou essa postagem AQUI, de nosso blog. Pois, para essa poligonal sei que a mesma está dentro da tolerância e não é objetivo dessas postagens a explicação sobre a Tolerância Angular. Cabe ressaltar que, levantamentos fora da Tolerância Angular devem a via de fato e dúvidas serem refeitos por completo, ou, para profissionais que dominam o Ajustamento das Observações a aplicação de Testes para determinar se houveram erros em um ou mais vértices para retornar a campo e realizar novamente as medidas apenas nos vértices que apresentaram erros, como por exemplo, com o Teste de Baarda.
Vamos então para a Correção Angular.
Correção Angular (Ca)
O erro angular é distribuído equitativamente para todos os vértices da poligonal. A correção ângular deve ser em sinal contrário do erro angular. Assim a Correção Angular é expressa:
Em que:
n = nº de vértices da poligonal.
No Excel:
Agora, ao tentar fazer a "estética" de nossa planilha chegaremos a um, bug, valor bem louco...
Isso ocorre pelo fato da nossa equação de transformação de Grau Decimal para Arco Sexagesimal só trabalhar com valores positivos, como a correção angular foi negativa esse bug aconteceu, mas, relaxem que é bem simples de ser resolvido.
Vamos utilizar a Função ABS, que retorna o valor absoluto de um número expresso na célula. Como também vamos realizar uma adaptação. Nota: Esse desenvolvimento foi eu que fiz, não vi em nenhum lugar essa metodologia, em resumo: Sou foda!!.
Sabemos que:
Para o valor do Grau usamos: INT(Grau Decimal);
Para o valor dos Minutos usamos: INT((Grau Decimal - INT(Grau Decimal))*60); e
Para o valor dos Segundos usamos: ((Grau Decimal - INT(Grau Decimal)*60 - INT((Grau Decimal - INT(Grau Decimal))*60))*60
Para trabalhar com valores negativos temos que adaptar, no caso:
Para o valor do Grau usamos: -(INT(ABS(Grau Decimal)));
Para o valor dos Minutos usamos: -(INT((ABS(Grau Decimal) - (INT(ABS(Grau Decimal))))*60)); e
Para o valor dos Segundos usamos: ((Grau Decimal - INT(Grau Decimal)*60 - INT((Grau Decimal - INT(Grau Decimal))*60))*60. Isso mesmo, para o cálculo dos segundos, não tem alteração na fórmula.
Percebam, em todos os valores eu informei para calcular o valor absoluto (módulo), ou seja, positivo da célula selecionada, e então com toda a fórmula fechada entre parênteses inseri o valor negativo para que o resultado fosse dado de acordo com o valor real.
Aplicando essa parada toda no Excel (para o grau e minuto), é bem simples, pois só iremos alterar o que já temos, vejamos:
Pressionando ENTER, o resultado será mostrado conforme.
Pronto, agora vamos ao próximo passo para finalizar esta etapa de nossa planilha e esta postagem.
Ângulos Horizontais Corrigidos
A os ângulos horizontais corrigidos são feitos de forma direta, pois, como temos o valor da correção angular por vértice basta somar esta a cada ângulo medido no levantamento.
Voltando ao Excel, vamos então inserir as quatro colunas referentes aos ângulos horizontais corrigidos (Grau, Minuto, Segundo e Grau Decimal).
Então agora vamos inserir a equação para calcular cada ângulo horizontal corrigido.
Já esteticamente formatada essa linha.
Agora para completar as demais células referentes aos ângulos horizontais corrigidos, não podemos apenas arrastar para baixo a fórmula declarada em K4, isso se deve ao fato do Excel entender que ao arrastar uma fórmula de uma célula de cima para uma de baixo, os valores ao qual ele irá buscar também irão descer, por exemplo:
Vejam que ao arrastarmos apenas uma célula para baixo, o Excel entendeu que, o ângulo também desceria uma célula e como as células dos ângulos horizontais e ângulos horizontais corrigidos, são iguais, no caso, tem a mesma configuração, ou seja, são um mesclado de duas linhas e estão na mesma posição, corretamente a fórmula declarada ao descer foi buscar o valor na célula correta, enquanto que a correção angular, por não ser configurada igual a célula do ângulo horizontal corrigido, desceu duas linhas, indo então para uma célula que estava vazia, causando um erro no cálculo.
E aí, como resolvemos isso?... Bem simples pessoas, como nessa situação, a correção angular é a mesma para todos os ângulos horizontais, vamos fixar a célula da correção angular na declaração da fórmula.
E como fixamos uma célula em uma equação do Excel?... Inserindo o símbolo $ antes da referência da coluna e $ antes da referência da linha.
No caso de nossa planilha, a correção angular encontra-se na célula G26, assim, para fixarmos ela na declaração da fórmula do ângulo horizontal corrigido, fazemos: $G$26.
Simples, não!
Fazendo isso o Excel vai entender que só irá mudar o ângulo, porém a correção será a mesma para todos os ângulos, então agora basta clicar na célula que acabamos de declarar a fórmula e então arrastar para baixo.
Pronto, para finalizar vamos arrastar as fórmulas para a conversão em arcos sexagesimais.
Com isso, esta etapa dos cálculos é finalizada. Agora em nossa Planilha de Cálculos, temos: O Erro angular, a Correção angular e os Ângulos horizontais corrigidos.
Então galera, espero que vocês tenham conseguido acompanhar e chegado até aqui junto comigo. Na próxima postagem, vamos realizar o cálculo dos Azimutes dos Alinhamentos.












































Professor seria possível o senhor disponibilizar estas planilhas?
ResponderExcluir