Excel aplicado a Topografia: Azimutes dos Alinhamentos

Para dar sequência ao nosso minicurso, mas, mini mesmo, de Excel Aplicado a Topografia, no caso aplicação desta ferramenta para o cálculo de uma poligonal topográfica fechada, vamos hoje, realizar o cálculo dos azimutes dos alinhamentos.

Então, para relembrar o Azimute é o ângulo horário medido da direção norte ao alinhamento, varia de 0° (zero graus) a 360° (trezentos e sessenta graus). O cálculo dos azimutes é uma etapa importante no desenvolvimento do cálculo de poligonal topográfica, por isso essa postagem é toda dedicada apenas a este cálculo.

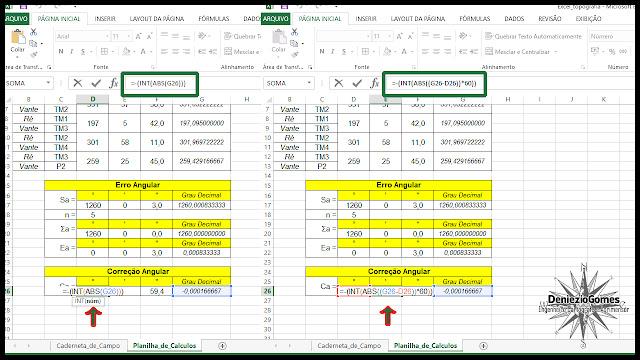
Pois bem, nossa planilha encontra-se neste ponto, já realizamos o cálculo da caderneta de campo, como também já temos o erro angular, a correção angular e os ângulos horizontais corrigidos:

Partindo deste ponto que ficamos, vamos então iniciar o cálculo dos azimutes.

Quando realizamos um levantamento planimétrico pelo método da poligonação, temo que ter a priori um Azimute de partida, este pode ser determinado em campo através da determinação do Norte Verdadeiro ou Magnético (mais comum), ou, quando se dispõe das coordenadas de pelo menos dois pontos próximo a área levantada. E esse foi o nosso caso.

Vejamos, em nosso levantamento tínhamos disponíveis dois pontos cujos as coordenadas eram conhecidas, os Marcos P₂ e P₃:

Sabendo disso, utilizamos o Marco P₃ como ponto de auxilio e o Marco P₂ como parte de nossa poligonal.

Em campo, estacionamos a Estação Total sobre o Marco P₂ e zeramos a mesma no Marco P₃ e pegamos o ângulo horário que tínhamos até o vértice TM₁. Com isso, determinamos o ângulo de orientação de nossa poligonal. Assim, com as coordenadas dos Pontos P₂ e P₃ e o ângulo de orientação da poligonal, temos um Azimute de partida como também podemos calcular os azimutes de nossa poligonal.

Então, a primeira ação é o cálculo do azimute entre o alinhamento P₃-P₂, pois este é o azimute de partida de nossa poligonal.

Vamos então para aquela revisão básica, pois vamos determinar o azimute de um alinhamento em função das coordenadas entre dois pontos. Quando dispomos das coordenadas de dois pontos de um alinhamento o azimute é determinado em função do cálculo Rumo (que é o menor ângulo formado entre o alinhamento e a linha Norte/Sul) e uma constante que vai variar de acordo com o quadrante que este Rumo se encontra.

Em resumo:

Assim, de acordo com a imagem acima, fica evidenciado que o azimute é o Rumo adicionado a uma constante que varia dependendo em qual quadrante esse alinhamento se encontra (rumo), e a determinação desse quadrante vai de acordo com a diferença entre as coordenadas dos dois pontos desse alinhamento ou seja, final e inicial.

Deste modo, com nossa planilha aberta vamos iniciar os cálculos de hoje.

Azimute de Partida (Az_P3-P2)

A primeira ação que tomaremos é COPIAR (ctrl+c) os dados do ângulo de orientação e coordenadas dos pontos P₃ e P₂ da Caderneta_de_Campo e COLAR (ctrl+v) para a Planilha_de_Calculos. (Aqueles que não criaram uma outra planilha e na aula passada continuaram os cálculos sobre a Caderneta de Campo não precisam realizar esta etapa.)

Feito isso, agora vamos determinar o ΔE e o ΔN, para definirmos em qual quadrante o rumo do alinhamento P₃-P₂ se encontra, para utilizarmos uma das quatro constantes e assim determinar o azimute do alinhamento (Aqui começa quem está trabalhando somente com a Caderneta_de_Campo).

ΔE = E_P2 - E_P3
ΔN = N_P2 - N_P3
Percebam que a diferença entre as coordenadas (Δ) é sempre dada pela coordenada do ponto de chegada (final) menos a coordenada do ponto de partida (inicial), como nosso alinhamento é P₃-P₂ ou seja parte-se do P₃ e chega-se no P₂ nossa fórmula resultou no que foi descrito acima.

No Excel:

Resultando:

Com o resultado encontrado ΔE e ΔN positivos, sabemos que o Rumo é do quadrante NE e assim o Azimute é igual ao Rumo, poderíamos apenas aplicar a fórmula para a determinação do Azimute, mas, a minha ideia aqui é automatizar, para que vocês em um futuro precisem utilizar esta fórmula para um rumo em outro quadrante não precisem realizar alterações, pois ela vai servir para os quatro.

Vemos que a fórmula do Azimute vai depender em que quadrante o rumo se encontra e a partir daí temos que somar uma das quatro constantes, então de certa forma devemos realizar um teste lógico, porém a Função SE por si só não dará conta desta solução, pois temos duas variáveis o ΔE e o ΔN, ou seja, duas condições e a Função SE só trabalha com uma condição retornando um resultado se essa condição for Verdadeira ou Falsa. Com isso iremos utilizar uma variante da Função SE que é a Função SE com E (SE(E)). Com essa função podemos verificar mais de uma condição e o resultado retornado se dará em conta da obtenção verdadeira ou falsa das duas condições impostas.

Por exemplo, para nosso caso o Rumo é do quadrante NE se ΔE for positivo e ΔN também for positivo, caso contrário ele é de um dos outros três quadrantes, no caso, ΔE positivo e ΔN negativo = quadrante SE, ΔE negativo e ΔN negativo = quadrante SO e ΔE negativo e ΔN positivo = quadrante NO. Assim temos que adaptar de modo que ele calcule as quatro condições.

Formulando no Excel temos:

SE(E(ΔE>0;ΔN>0);Graus(atan(ΔE/ΔN);SE(E(ΔE>0;ΔN<0);Graus(atan(ΔE/ΔN))+180;SE(E(ΔE<0;ΔN<0);Graus(atan(ΔE/ΔN))+180;SE(E(ΔE<0;ΔN>0);Graus(atan(ΔE/ΔN))+360))))
Embora pareça ser um quebra cabeça, essa formulação é bem simples de ser entendida, praticamente estou mandando o Excel:

• Verificar se o ΔE é positivo e o ΔN também é positivo, caso essa afirmação seja verdadeira ele vai calcular: Graus(Atan(ΔE/ΔN)) Nota: a declaração Graus( é a maneira de converter um valor que está em radianos para grau decimal no Excel, temos que declarar dessa forma pois como já explicado o Excel diferentemente de nossas calculadoras de mão, não faz essa conversão automaticamente.
• Não sendo afirmativas as duas condições anteriores o Excel então vai verificar se ΔE é positivo e o ΔN é negativo, caso verdadeiro, então: Graus(atan(ΔE/ΔN))+180;
• Novamente não tendo as duas condições afirmativas, o Excel vai verificar a terceira hipótese que é ΔE é negativo e ΔN também negativo, caso essa hipótese seja verdadeira: Graus(atan(ΔE/ΔN))+180;
• Por fim, nenhuma das três hipóteses anteriores não sendo verdadeira, o Excel verificará a última que é ΔE é negativo e o ΔN positivo, calculando assim o Azimute por: Graus(atan(ΔE/ΔN))+360.

No excel, eu recomendo fazermos o seguinte, para não ter dor de cabeça nem correr riscos de errar essa fórmula gigantesca.

Primeiro cálculamos o rumo, para isso vamos criar um espaço reservado para ele em nossa planilha.

Cálculando o rumo pela fórmula: rumo = Graus(atan(ΔE/ΔN)

Com o Rumo cálculado agora vamos reservar um espaço para as constantes e inserí-las:

Para finalizar, então agora vamos inserir a fórmula do Azimute em um espaço reservado.

E como resultado:

Como já era esperado, pelo fato do alinhamento está no primeiro quadrante, o Azimute é igual ao Rumo.

Cálculado o Azimute de Partida, agora fácilmente calculamos os azimutes dos alinhamentos de nossa poligonal, que é objetivo principal dessa nossa postagem.

Azimutes dos Alinhamentos

Dispondo de um azimute de partida e direções (ângulos horizontais), o azimute de um alinhamento é definido como:

Az_n = Az_n-1 + α ± 180°
Az_n = Az_n-1 - α ± 180°
Em que:

Az_n = Azimute do alinhamento;
Az_n-1 = Azimute do alinhamento anterior;
α = Ângulo horizontal medido. Soma-se α quando o Ângulo horizontal foi medido no sentido horário e subtrai-se α quando o Ângulo horizontal foi medido no sentido anti-horário.
± 180° = soma-se 180° quando (Az_n-1 + α)<180° ou (Az_n-1 - α)<180°, e, subtrai-se 180° quando (Az_n-1 + α)>180° ou (Az_n-1 - α)>180°

Em nosso caso, como os ângulos foram medidos no sentido horário, como consta na primeira postagem dessa série, o azimute dos alinhamentos será dado pela primeira equação: Az_n = Az_n-1 + α ± 180°

Percebe-se que como temos a opção somar ou subtrair 180° devemos inserir uma equação lógica, por ser apenas uma condição podemos facilmente usar a Função SE.

MAS, ATENÇÃO!!

O azimute do primeiro alinhamento (P₂-TM₁) deve ser calculado em função do Azimute P₃-P₂. Isso se deve pelo fato de não termos o conhecimento das coordenadas dos vértice TM₄ e, justamente por isso, utilizamos o Marco P₃ como auxiliar, determinando assim um ângulo de orientação para nossa poligonal.

Agora sem enrolação vamos ao Excel, começar os cálculos, primeiro, vamos criar o espaço para os Azimutes dos Alinhamentos.

Agora vamos ao cálculo do Azimute P₂-TM₁:

Discriminando a declaração da imagem, praticamente estou dizendo que o Azimute P₂-TM₁ = Azimute de Anterior (Azimute P₃-P₂) + Ângulo Horário (Ângulo de Orientação) ± 180° (que vai variar dependendo da condição imposta, no caso como condição coloquei que se a soma do azimute anterior + o ângulo horário for maior que 180° ele vai subtrair 180° se não, ele vai somar 180°).

E como resultado temos:

Agora percebam, o azimute é um Ângulo que vária de 0° a 360°, no caso do primeiro cálculo o valor do azimute deu dentro desse intervalo, mas, o que aconteceria se o valor estivesse fora desse intervalo?

Bem simples, no caso por esse modelo matemático (soma de azimute com ângulos) o azimute só pode ficar fora do intervalo para mais, ou seja, maior que 360°, quando isso acontecer, subtraímos 360° do valor final. No Excel, podemos novamente usar a Função SE, para determinar essa condição, ou seja:

SE((Az_n = Az_n-1 + α ± 180°)>360°;(Az_n = Az_n-1 + α ± 180°)-360°;(Az_n = Az_n-1 + α ± 180°))
Estou dizendo que:

Se o Az>360° ele vai subtrair 360°, se não, ele vai deixar do jeito que estar.

Inserindo no Excel, na célula que já temos declarado a fórmula:

Como o Azimute calculado não era maior que 360°, ele deixou do jeito que estava.

Agora vamos aos azimutes dos demais alinhamentos, primeiro de TM₁-TM₂. Sem a condição dos 360°.

Agora inserindo a condição dos 360°.

Como resultado temos:

Para os demais azimutes, vamos fazer a mágica do Excel, simplesmente clicando na célula que acabamos de preencher e arrastamos para as demais que faltam.

Repetindo para conversão em Arco:

Com isso, o cálculo dos azimutes dos alinhamentos está finalizado, mas, como ter certeza que os cálculos estão certos?

Basta recalcular o azimute do alinhamento P₂-TM₁, como a poligonal é fechada, o azimute anterior agora será o azimute do alinhamento TM₃-TM₄ (191°46'39,6") e o ângulo, o ângulo horizontal medido que foi zerado em TM₄ com vante em TM₁ (169°52'28,4") e a Estação em P₂, como estaremos utilizando dados diferentes, se o azimute calculado a partir desses dados der igual ao azimute calculado a partir do azimute P₃-P₂ e do ângulo de orientação, mostra que nosso cálculo está correto.

Fazendo:

Resultando:

Como esperado os resultados bateram.

Assim terminamos essa postagem, espero que todos tenham conseguido acompanhar até aqui. Em nossa próxima aula iremos calcular as Projeções, determinar o Erro Linear, as Correções das Projeções e Calcular as Projeções Corrigidas.

◀ AULA ANTERIOR

PRÓXIMA AULA ▶

Leia mais

Excel aplicado a Topografia: Erro Angular, Correção Angular e Ângulos Horizontais Corrigidos

Então pessoas, tudo beleza?

Vamos dar sequência ao nosso minicurso de Excel aplicado a Topografia, mais precisamente em como realizar um cálculo de uma poligonal fechada com essa ferramenta. O interessante é que, com os conhecimentos adquiridos neste minicurso, vocês facilmente poderão aplicar em outros métodos topográficos o que aprenderem aqui.

Para hoje, vamos iniciar a nossa Planilha de Cálculos com a determinação do Erro Angular, da Correção Angular e por fim os Ângulos Horizontais Corrigidos.

Pois bem, vamos ao que interessa.
De início, abram a nossa pasta de trabalho no Excel, que deve estar assim:

Agora com nossa planilha aberta, tem-se duas opções: 1 - Continuar nessa planilha e dar sequência aos cálculos, ou, 2 - Criar uma nova planilha dentro dessa pasta de trabalho.

Pessoalmente eu prefiro criar uma nova planilha, e assim eu o farei. E esta nova planilha chamarei de Planilha_de_Calculo. E para isso basta clicar nesse símbolo de + ao lado da aba em que se encontra a planilha da Caderneta_de_Campo.

Aqueles que preferirem continuar na mesma planilha pulem esta etapa e vão onde realmente começamos a trabalhar.

Fazendo isso, basta então inserir o nome da nova planilha clicando duas vezes sobre o nome plan1. Ao final a planilha de vocês deve se encontrar assim.

OBS: Eu não coloquei acento agudo por analfabetismo funcional não galera, o motivo é que não é recomendado inserir caracteres especiais em nomes de arquivos de determinados softwares e as planilhas eletrônicas estão nessa lista.

Agora sim, vamos começar a trabalhar (aqueles que pularam começam aqui) nossa planilha de cálculos.

Para iniciar vamos reescrever os dados que realmente iremos utilizar da Caderneta de Campo para nossa Planilha de Cálculos, no caso vamos copiar as colunas A, B e C da Caderneta_de_Campo e colar na Planilha_de_Calculos.

Como também iremos copiar as colunas P, Q, R e S da Caderneta_de_Campo e colar na Planilha_de_Calculos.

Percebam que ao fazer isto, o resultado das células ficaram com vários erros. Isso se deve ao fato de termos fórmulas declaradas nas colunas P, Q, R e S, e na nova planilha essas fórmulas estão endereçadas para dados que não existem nela. Mas, sem esquentar a cabeça facilmente resolvemos este problema.

Basta ir na Célula G4 que está mesclada com a G5 (Planilha_de_Calculos), e digitar =, na sequência, vamos na Caderneta_de_Campo e clicamos sobre a Célula S4 que está mesclada com a célula S5, por fim pressionamos enter.

Ao darmos enter, o ângulo horizontal correto em grau decimal aparece na célula G4/G5, como também em arco sexagesimal, já que nestas células o endereçamento dessas células são para a célula do grau decimal.

Para as demais células dessa coluna, basta selecionar a primeira e arrastar para baixo, que teremos um auto preenchimento.

Pronto. Agora vamos iniciar realmente os cálculos de nossa planilha.

Como inicialmente iremos trabalhar com os dados angulares de nossa poligonal, os dados lineares (distâncias) serão copiados para a planilha de cálculos posteriormente.

Erro Angular E_a

Para quem me acompanha aqui no blogger ou no YouTube, já tem o conhecimento de que em uma poligonal geometricamente fechada (E_a = 0), a soma dos ângulos, no sistema sexagesimal, obedece a uma das seguintes fórmulas:

Σ_ai = 180° * (n-2) → Para ângulos internos a poligonal.
Σ_ae = 180° * (n+2) → Para ângulos externos a poligonal.

Em que: n = nº de vértices da poligonal.

A não ser que vocês acochambrem umas paradas, é evidente que o somatório dos ângulos medidos em campo vai discrepar do resultado do somatório dado por umas das fórmulas acima. Essa diferença é o que chamamos de Erro Angular.

Assim, o erro angular é dado:

E_a = S_a - Σ_a
Em que:
S_a = somatório dos ângulos medidos em campo;
Σ_a = somatório angular de uma poligonal geométricamente fechada.

Sabendo disso, vamos jogar essas fórmulas em nossa Planilha.

Para o S_a usaremos a Função SOMA do Excel, onde, basta na célula onde queremos identificar esse valor digitar =SOMA(Selecionar as células que deseja fazer a soma)

Nota: clicamos na primeira célula, pressionamos SHIFT e clicamos na última célula.

E por fim pressionamos enter.

Agora por estética, vamos preencher as colunas D, E e F da linha 17, no caso inserirmos as fórmulas de conversão de Grau Decimal para arco sexagesimal. Para isso, vamo apenas copiar da Caderneta_de_Campo e colar na Planilha_de_Cálculo.

Para o Σ_a vamos apenas replicar a fórmula no Excel, só temos que atentar ao seguinte, neste, precisamos do número de vértices. Aí fica a seu critério, digitar logo o valor, ou declarar n em uma célula, para automatizar a parada eu vou na segunda opção.

Para isso, vamos utilizar a Função CONT.valores, essa função conta o número de células não vazias, assim, usando ela e selecionando as células das estações, que são iguais ao números de vértices, ela chegará ao número de vértices de nossa poligonal, após pressionar ENTER.

Agora vamos aplicar a fórmula do somatório dos ângulos de uma poligonal geométricamente fechada, lembrando que para nosso caso os angulos medidos foram externos a poligonal como citado no post anterior. Assim:

Σ_ae = 180° * (n+2)
No Excel:

Desta forma, já temos o S_a e o Σ_a podemos calcular o Erro Ângular (E_a).

Com isso calculamos o Erro Angular cometido em nosso levantamento. Destaco aqui, que após a determinação do Erro Angular, precisamos verificar a Tolerância Angular para o Levantamento, ou seja, o que é tolerável errar angularmente. Esta tolerância, depende do número de vértices e da precisão angular do equipamento utilizado no levantamento, para mais informações sobre tolerância angular recomendo que leiam a NBR 13133, ou essa postagem AQUI, de nosso blog. Pois, para essa poligonal sei que a mesma está dentro da tolerância e não é objetivo dessas postagens a explicação sobre a Tolerância Angular. Cabe ressaltar que, levantamentos fora da Tolerância Angular devem a via de fato e dúvidas serem refeitos por completo, ou, para profissionais que dominam o Ajustamento das Observações a aplicação de Testes para determinar se houveram erros em um ou mais vértices para retornar a campo e realizar novamente as medidas apenas nos vértices que apresentaram erros, como por exemplo, com o Teste de Baarda.

Vamos então para a Correção Angular.

Correção Angular (C_a)

O erro angular é distribuído equitativamente para todos os vértices da poligonal. A correção ângular deve ser em sinal contrário do erro angular. Assim a Correção Angular é expressa:

C_a = -(E_a/n)
Em que:
n = nº de vértices da poligonal.

No Excel:

Agora, ao tentar fazer a "estética" de nossa planilha chegaremos a um, bug, valor bem louco...

Isso ocorre pelo fato da nossa equação de transformação de Grau Decimal para Arco Sexagesimal só trabalhar com valores positivos, como a correção angular foi negativa esse bug aconteceu, mas, relaxem que é bem simples de ser resolvido.

Vamos utilizar a Função ABS, que retorna o valor absoluto de um número expresso na célula. Como também vamos realizar uma adaptação. Nota: Esse desenvolvimento foi eu que fiz, não vi em nenhum lugar essa metodologia, em resumo: Sou foda!!.

Sabemos que:

Para o valor do Grau usamos: INT(Grau Decimal);
Para o valor dos Minutos usamos: INT((Grau Decimal - INT(Grau Decimal))*60); e
Para o valor dos Segundos usamos: ((Grau Decimal - INT(Grau Decimal)*60 - INT((Grau Decimal - INT(Grau Decimal))*60))*60

Para trabalhar com valores negativos temos que adaptar, no caso:

Para o valor do Grau usamos: -(INT(ABS(Grau Decimal)));
Para o valor dos Minutos usamos: -(INT((ABS(Grau Decimal) - (INT(ABS(Grau Decimal))))*60)); e
Para o valor dos Segundos usamos: ((Grau Decimal - INT(Grau Decimal)*60 - INT((Grau Decimal - INT(Grau Decimal))*60))*60. Isso mesmo, para o cálculo dos segundos, não tem alteração na fórmula.

Percebam, em todos os valores eu informei para calcular o valor absoluto (módulo), ou seja, positivo da célula selecionada, e então com toda a fórmula fechada entre parênteses inseri o valor negativo para que o resultado fosse dado de acordo com o valor real.

Aplicando essa parada toda no Excel (para o grau e minuto), é bem simples, pois só iremos alterar o que já temos, vejamos:

Pressionando ENTER, o resultado será mostrado conforme.

Pronto, agora vamos ao próximo passo para finalizar esta etapa de nossa planilha e esta postagem.

Ângulos Horizontais Corrigidos

A os ângulos horizontais corrigidos são feitos de forma direta, pois, como temos o valor da correção angular por vértice basta somar esta a cada ângulo medido no levantamento.

α = α_campo + C_a
Voltando ao Excel, vamos então inserir as quatro colunas referentes aos ângulos horizontais corrigidos (Grau, Minuto, Segundo e Grau Decimal).

Então agora vamos inserir a equação para calcular cada ângulo horizontal corrigido.

Já esteticamente formatada essa linha.

Agora para completar as demais células referentes aos ângulos horizontais corrigidos, não podemos apenas arrastar para baixo a fórmula declarada em K4, isso se deve ao fato do Excel entender que ao arrastar uma fórmula de uma célula de cima para uma de baixo, os valores ao qual ele irá buscar também irão descer, por exemplo:

Vejam que ao arrastarmos apenas uma célula para baixo, o Excel entendeu que, o ângulo também desceria uma célula e como as células dos ângulos horizontais e ângulos horizontais corrigidos, são iguais, no caso, tem a mesma configuração, ou seja, são um mesclado de duas linhas e estão na mesma posição, corretamente a fórmula declarada ao descer foi buscar o valor na célula correta, enquanto que a correção angular, por não ser configurada igual a célula do ângulo horizontal corrigido, desceu duas linhas, indo então para uma célula que estava vazia, causando um erro no cálculo.

E aí, como resolvemos isso?... Bem simples pessoas, como nessa situação, a correção angular é a mesma para todos os ângulos horizontais, vamos fixar a célula da correção angular na declaração da fórmula.

E como fixamos uma célula em uma equação do Excel?... Inserindo o símbolo $ antes da referência da coluna e $ antes da referência da linha.

No caso de nossa planilha, a correção angular encontra-se na célula G26, assim, para fixarmos ela na declaração da fórmula do ângulo horizontal corrigido, fazemos: $G$26.

Simples, não!

Fazendo isso o Excel vai entender que só irá mudar o ângulo, porém a correção será a mesma para todos os ângulos, então agora basta clicar na célula que acabamos de declarar a fórmula e então arrastar para baixo.

Pronto, para finalizar vamos arrastar as fórmulas para a conversão em arcos sexagesimais.

Com isso, esta etapa dos cálculos é finalizada. Agora em nossa Planilha de Cálculos, temos: O Erro angular, a Correção angular e os Ângulos horizontais corrigidos.

Então galera, espero que vocês tenham conseguido acompanhar e chegado até aqui junto comigo. Na próxima postagem, vamos realizar o cálculo dos Azimutes dos Alinhamentos.

◀ AULA ANTERIOR

PRÓXIMA AULA ▶

Leia mais