1. INTRODUÇÃO
De acordo com Comastri (1977), medir uma grandeza envolve compará-la com outra grandeza de mesma natureza e determinar quantas vezes ela é maior ou menor em relação à grandeza de referência. A unidade de medida é a porção da grandeza usada como ponto de comparação. O valor numérico que indica quantas vezes a grandeza é maior ou menor que a unidade escolhida é chamado de medida da grandeza. Portanto, a medição de uma grandeza, seja linear ou angular, implica em determinar quantas vezes a grandeza em questão contém a unidade de medida escolhida.
Por exemplo, se um segmento de linha AB no terreno contém 10 vezes a unidade de um metro, o comprimento medido AB é 10 vezes maior que a unidade, e podemos afirmar que o comprimento é de 10 metros, representado como AB = 10m. Da mesma forma, se um ângulo AOB contém 15 vezes a unidade grau, o ângulo medido é de 15°, e podemos escrever AÔB = 15°.
2. SISTEMA INTERNACIONAL DE UNIDADES
A necessidade de realizar medições é uma prática ancestral que remonta aos primórdios das civilizações. Durante um longo período, cada país e região desenvolveu seu próprio sistema de medidas, muitas vezes utilizando unidades arbitrárias e imprecisas, como o palmo, pé, polegada, braça e côvado, frequentemente baseadas nas dimensões do corpo humano. Essa diversidade de sistemas de medida criava consideráveis desafios para o comércio, pois as pessoas de uma região não estavam familiarizadas com as unidades de medida adotadas em outras regiões.
Em 1789, uma tentativa de abordar esse desafio levou o Governo Republicano Francês a solicitar à Academia de Ciências da França a criação de um sistema de medidas fundamentado em uma "constante natural". Isso culminou na criação do Sistema Métrico Decimal. Com o tempo, vários países, incluindo o Brasil em 1928, aderiram à "Convenção do Metro" e passaram a adotar esse sistema. Inicialmente, o Sistema Métrico Decimal consistia em três unidades básicas de medida: o metro, o litro e o quilograma.
No entanto, devido ao avanço da ciência e da tecnologia, as necessidades de medições mais precisas e diversificadas cresceram. Como resultado, em 1960, o Sistema Métrico Decimal foi substituído pelo Sistema Internacional de Unidades - SI, também conhecido como Sistema Internacional de Medidas. O SI é mais complexo e sofisticado, e o Brasil o adotou em 1962, ratificado pela Resolução nº 12 de 1988 do Conselho Nacional de Metrologia, Normalização e Qualidade Industrial - Conmetro, tornando seu uso obrigatório em todo o Território Nacional.
Hoje o SI tem sete unidades de base: o metro – m (comprimento), o quilograma – kg (massa), o segundo – s (tempo), o ampere - A (intensidade de corrente elétrica), o kelvin – k (temperatura termodinâmica), o mol (quantidade de substância) e a candela – cd (intensidade luminosa).
Trata-se de um sistema prático, coerente e mundialmente aceito nas relações internacionais, no ensino e nas pesquisas científicas, que evolui continuamente para refletir as melhores práticas de medição. O SI é o sistema de unidades adotado por todos os países do mundo, com exceção da Birmânia, da Libéria e dos Estados Unidos.
Para o contexto da Topografia, nesta postagem, serão tratadas três espécies de medidas:
3. MEDIDAS LINEARES
No Brasil, a unidade fundamental para a medição de comprimento é o metro, o qual é uma das sete unidades fundamentais do Sistema Internacional de Unidades (SI).
A unidade de medida chamada "metro" foi definida como sendo a vigésima milionésima parte (1/20.000.000) do comprimento de um quarto do meridiano terrestre (Comastri, 1977).
Atualmente, o metro é definido como o comprimento que a luz percorre no vácuo durante um período de tempo igual a 1/299.792.458 de segundos, conforme estabelecido como a 17ª unidade base pelo Comitê Geral de Pesos e Medidas (CGPM) em 1983.
Nota: A “Conference Générale des Poids et Mesures’ (Conferência Geral de Pesos e Medidas ou CGPM) é uma das três organizações criadas para avaliar e gerir o sistema Internacional de Unidades (SI) nos termos da “Metre Convention” (1875). Reúne-se em Paris a cada quatro ou seis anos.”
A unidade primária de medida de comprimento é o metro; no entanto, em algumas situações, essa unidade pode se tornar impraticável. Por exemplo, quando a medição envolve uma extensão muito grande, o metro pode ser considerado muito pequeno para essa finalidade. Por outro lado, em medições que envolvem extensões muito pequenas, o metro pode ser considerado excessivamente grande. Para contornar esse problema, o sistema métrico utiliza múltiplos e submúltiplos do metro.
Além das unidades de medidas oficiais apresentadas, cabe mostrarmos outras unidades mais antigas, a exemplo:
* Neste caso o raio médio da Terra tem valor aproximado de 6.366.707,02 m.
Exemplo 001: Converta para metros os seguintes valores:
a) 15.000 mm
b) 120 dam
c) 0,01 km
d) 1283 cm
e) 17 hm
f) 120 dm
g) 1.550.055 mm
h) 3.871 cm
i) 210 dam
j) 201 dm
3.1 Tipos de medidas lineares
As medidas lineares podem ser de três tipos.
DH = Distância Horizontal
DV = Distância Vertical
DI = Distância Inclinada
3.1.1 Horizontais
Referem-se às distâncias medidas em paralelo a um plano horizontal de referência. Essas medidas são utilizadas em Levantamentos Topográficos Planimétricos.
3.1.2 Verticais
Representam as distâncias medidas perpendicularmente a um plano horizontal de referência. Essas medidas são empregadas para quantificar as diferenças de altitude entre elementos da superfície e são fundamentais em Levantamentos Topográficos Altimétricos ou Planialtimétricos.
3.1.3 Inclinadas
Refere-se à medida de distância entre dois pontos em planos que seguem a inclinação da superfície do terreno.
3.2 Equipamentos de medição linear
3.2.1 Trena
É possível realizar medições em todas as direções. O material do qual pode ser composta a haste de medição inclui opções como fibra de vidro, aço com correção de temperatura (recomendada) e ínvar, que é a opção ideal.
Fonte: MSMI, s.d.
3.2.2 Mira (regua graduada)
Instrumento auxiliar empregado para determinar distâncias horizontais e verticais com o auxílio de um teodolito.
3.2.3 Distanciômetro
É um dispositivo eletrônico que utiliza tecnologia a laser (Light Amplification by Stimulated Emission of Radiation) ou infravermelho para medir distâncias entre o equipamento e uma superfície refletora, frequentemente utilizando um prisma como alvo de reflexão.
Fonte: AllComp, s.d.
3.2.4 Estação Total (teodolito + distanciômetro)
Da mesma forma que o distanciômetro, a Estação Total é um dispositivo eletrônico que usa tecnologia a laser ou infravermelho para medir distâncias entre o equipamento e uma superfície refletora, frequentemente um prisma. Além disso, a estação total também é capaz de medir ângulos.
Fonte: CPE, s.d.
4. MEDIDAS ANGULARES
Medidas angulares podem ser realizadas nos planos horizontal (o horizonte do instrumento) e vertical (o plano que contém a linha vertical do local). Dessa forma, temos os ângulos horizontais e verticais (Veras, 2012).
Quando se trata de medições angulares em um plano bidimensional, o Sistema Internacional (SI) define três unidades de medida: grau, grado e radiano (Silva; Segantine, 2015).
Os instrumentos topográficos para medição de ângulos frequentemente utilizam como unidade de medida o grau ou o grado.
4.1 Grau
A unidade de medida conhecida como grau é uma unidade sexagesimal na qual a circunferência é dividida em 360 partes iguais, sendo cada uma dessas partes equivalente a um ângulo de 1 grau (1°). Cada grau, por sua vez, é subdividido em 60 partes iguais, e cada uma dessas partes corresponde a um ângulo de 1 minuto (1'). Cada minuto é então subdividido em 60 partes iguais, com cada uma delas representando um ângulo de 1 segundo (1”) (Silva; Segantine, 2015).
O valor de 1 grau é igual ao ângulo central que intercepta, em uma circunferência, um arco cujo comprimento corresponde a 1/360 do comprimento total da circunferência.
Na unidade sexagesimal de graus, os graus, minutos e segundos são representados pelo símbolo de grau para os graus, um acento agudo para os minutos e aspas para os segundos. Esses símbolos são colocados na parte superior direita dos números correspondentes (Silva; Segantine, 2015). Dessa forma:
175°23′44"
Lê-se: 175 graus, 23 minutos e 44 segundos.
O grau também pode ser representado usando uma segunda notação, chamada de notação decimal. Nessa forma numérica, estamos mais familiarizados, e o grau pode ser expresso como um número não inteiro. Por exemplo, o valor 175,3955556° (como mencionado anteriormente) pode ser simplificado para um único número decimal.
É viável converter valores entre as notações de grau decimal e sexagesimal. A notação decimal pode ser facilmente obtida a partir da notação sexagesimal usando a seguinte fórmula:
grau+min/60+seg/3600
Exemplo 002: Converta para graus decimais, os seguintes ângulos em graus sexagesimais:
a) 75°15’25”
b) 23°37’42”
c) 36°61’12”
d) 90°45’22,5”
e) 47°17'18"
f) 143°53’59”
g) 180°59’61”
h) 235°28’36”
i) 301°00”58”
j) 359°59’59”
Assim como é possível realizar a transformação de graus sexagesimais em graus decimais, o caminho inverso é dado pela seguinte formulação:
Exemplo 003: Converta para graus sexagesimais, os seguinte ângulo em graus decimais: 75,789532158°
Grau = 75°
Minutos = (75,789532158 - 75) * 60 = 47,37192948 ⇒ somente a parte inteira ⇒ 47'
Segundos = (47,37192948 - 47) * 60 = 22,31576880"
R. 75°47'22,32"
Exemplo 004: Converta para graus sexagesimais, os seguintes ângulos em graus decimais:
a) 181,660833333
b) 72,460000000
c) 15,236944444
d) 100,000277778
e) 359,033055556
f) 2,666388889
g) 63,755000000
h) 54,528888889
i) 48,373611111
j) 276,153055556
4.1.1 Equipamentos de medição angular
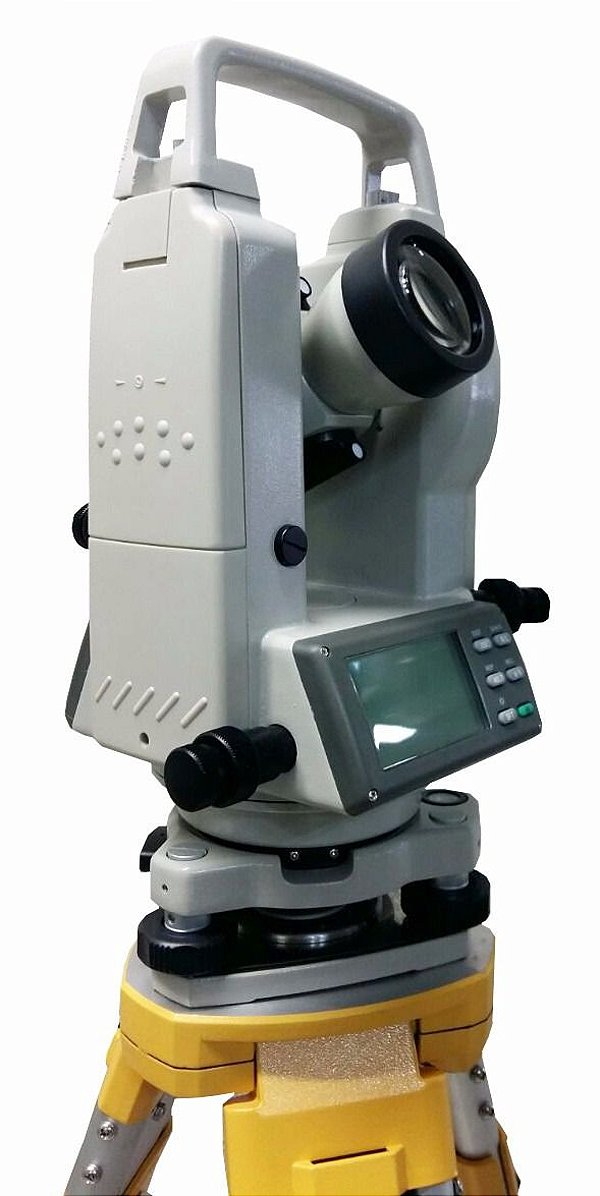
4.1.1.1 Teodolito
Um dispositivo empregado para medir com precisão ângulos tanto horizontais quanto verticais é conhecido como teodolito. Embora os teodolitos atuais sejam todos eletrônicos, ainda é comum o uso de teodolitos óptico-mecânicos.
Fonte: AllComp.
4.1.1.2 Estação Total
Assim como o teodolito, a estação total é capaz de medir ângulos tanto horizontais quanto verticais. A principal distinção entre elas e os teodolitos é que as estações totais também são capazes de medir distâncias. Importante notar que todas as estações totais são dispositivos eletrônicos e têm a capacidade de armazenar automaticamente as informações coletadas.
4.2 Grado
O valor de 1 grado corresponde ao ângulo central que intercepta um arco em uma circunferência, com um comprimento igual a 1/400 do comprimento total da circunferência.
Nesse contexto, a circunferência é dividida em 400 partes iguais, conforme ilustrado na figura, onde cada uma dessas partes representa um ângulo de 1g (um grado). Cada grado é subdividido em 100 partes iguais, com cada parte correspondendo a um ângulo de 1 centígrado ou 1 minuto centesimal. Além disso, cada centígrado ou minuto centesimal é subdividido em 100 partes iguais, onde cada uma delas equivale a um ângulo de 1 miligrado ou 1 segundo centesimal (Silva, Segantine, 2015).
Assim, 135,6342g corresponde a 135 grados, 63 centígrados e 42 miligrados ou 63 minutos centesimais e 42 segundos centesimais.
4.3 Relação entre grau e grado
A relação entre a medida de um ângulo em graus (°) e a mesma medida em grados (g) é determinada pela diferença entre as duas divisões, que são 360 e 400 partes (Veras, 2012). Portanto:
α°/αg = 360/400 = 9/10 ⇒ α° = 9/10αg
Exemplo 005: (Veras, 2012) Expressar no sistema sexagesimal o ângulo:
φ = 366g25′36"
φ° = (9/10)*366,2536g = 329°37'41,6"
Exemplo 006: Expressar no sistema sexagesimal o ângulo: φ = 283g37′10"
Exemplo 007: (Veras, 2012) Expressar no sistema centesimal o ângulo: φ = 165°15'40"
φg = (10/9)*165,2611111° = 183,6234568g = 183g62'34,568"
Exemplo 008: Expressar no sistema centesimal o ângulo: φ = 195°45'41"
4.4 Radianos
O valor de 1 radiano corresponde ao ângulo central que intercepta um arco de comprimento igual ao raio, quando consideramos uma circunferência com raio de 1 metro. Em outras palavras, um radiano é o ângulo central que corresponde a um arco de comprimento igual ao raio da circunferência.
Conforme ilustrado na figura abaixo, uma circunferência completa equivale a um ângulo de 2π radianos (6,283185 radianos), e um radiano corresponde a um ângulo de 57 graus, 17 minutos e 44,81 segundos. O ângulo reto, por sua vez, equivale a π/2 radianos. Devido ao fato de que o radiano expressa a relação entre dois comprimentos, ele é considerado uma unidade adimensional (Silva, Segantine, 2015).
4.5 Relação entre grau e radianos
Levando em consideração que o comprimento de uma circunferência com raio "r" é igual a 2πr, podemos estabelecer a seguinte relação:
2π𝑟/(360°) = c/α ⟹ α = (c×360°)/2π𝑟
Quando c = r ⟹ 1 radiano
α = 1rad = (180°)/π = 57°17'44,806"
Exemplo 009: (Veras, 2012) Expressar no sistema sexagesimal o ângulo: φ = 1,25614875rad
φ°=(180°)/π × 1,25614875 = 71°58'19,28"
Exemplo 010: Expressar no sistema radianos o ângulo: φ=257°00'15"
φrad = π/(180°) × 257°00′15" = 4,4855689
5 MEDIDAS SUPERFICIAIS
A unidade padrão para a medição de superfície no Sistema Internacional (SI) é o metro quadrado (m²). No entanto, em determinadas situações, é necessário utilizar múltiplos e submúltiplos dessa unidade.
Nas medidas agrárias, é comum utilizar uma unidade denominada "are" (a). O are possui o hectare (ha) como seu múltiplo e o centiare (ca) como seu submúltiplo.
Outras medidas usadas.
Por exemplo, se um segmento de linha AB no terreno contém 10 vezes a unidade de um metro, o comprimento medido AB é 10 vezes maior que a unidade, e podemos afirmar que o comprimento é de 10 metros, representado como AB = 10m. Da mesma forma, se um ângulo AOB contém 15 vezes a unidade grau, o ângulo medido é de 15°, e podemos escrever AÔB = 15°.
2. SISTEMA INTERNACIONAL DE UNIDADES
A necessidade de realizar medições é uma prática ancestral que remonta aos primórdios das civilizações. Durante um longo período, cada país e região desenvolveu seu próprio sistema de medidas, muitas vezes utilizando unidades arbitrárias e imprecisas, como o palmo, pé, polegada, braça e côvado, frequentemente baseadas nas dimensões do corpo humano. Essa diversidade de sistemas de medida criava consideráveis desafios para o comércio, pois as pessoas de uma região não estavam familiarizadas com as unidades de medida adotadas em outras regiões.
 |
| Fonte: MEDE, 2018. |
Em 1789, uma tentativa de abordar esse desafio levou o Governo Republicano Francês a solicitar à Academia de Ciências da França a criação de um sistema de medidas fundamentado em uma "constante natural". Isso culminou na criação do Sistema Métrico Decimal. Com o tempo, vários países, incluindo o Brasil em 1928, aderiram à "Convenção do Metro" e passaram a adotar esse sistema. Inicialmente, o Sistema Métrico Decimal consistia em três unidades básicas de medida: o metro, o litro e o quilograma.
No entanto, devido ao avanço da ciência e da tecnologia, as necessidades de medições mais precisas e diversificadas cresceram. Como resultado, em 1960, o Sistema Métrico Decimal foi substituído pelo Sistema Internacional de Unidades - SI, também conhecido como Sistema Internacional de Medidas. O SI é mais complexo e sofisticado, e o Brasil o adotou em 1962, ratificado pela Resolução nº 12 de 1988 do Conselho Nacional de Metrologia, Normalização e Qualidade Industrial - Conmetro, tornando seu uso obrigatório em todo o Território Nacional.
Hoje o SI tem sete unidades de base: o metro – m (comprimento), o quilograma – kg (massa), o segundo – s (tempo), o ampere - A (intensidade de corrente elétrica), o kelvin – k (temperatura termodinâmica), o mol (quantidade de substância) e a candela – cd (intensidade luminosa).
 |
| Fonte: Mundo Educação |
Trata-se de um sistema prático, coerente e mundialmente aceito nas relações internacionais, no ensino e nas pesquisas científicas, que evolui continuamente para refletir as melhores práticas de medição. O SI é o sistema de unidades adotado por todos os países do mundo, com exceção da Birmânia, da Libéria e dos Estados Unidos.
Para o contexto da Topografia, nesta postagem, serão tratadas três espécies de medidas:
- Lineares: COMPRIMENTO
- Angulares: ÂNGULOS
- Superfície: ÁREAS
3. MEDIDAS LINEARES
No Brasil, a unidade fundamental para a medição de comprimento é o metro, o qual é uma das sete unidades fundamentais do Sistema Internacional de Unidades (SI).
A unidade de medida chamada "metro" foi definida como sendo a vigésima milionésima parte (1/20.000.000) do comprimento de um quarto do meridiano terrestre (Comastri, 1977).
Atualmente, o metro é definido como o comprimento que a luz percorre no vácuo durante um período de tempo igual a 1/299.792.458 de segundos, conforme estabelecido como a 17ª unidade base pelo Comitê Geral de Pesos e Medidas (CGPM) em 1983.
Nota: A “Conference Générale des Poids et Mesures’ (Conferência Geral de Pesos e Medidas ou CGPM) é uma das três organizações criadas para avaliar e gerir o sistema Internacional de Unidades (SI) nos termos da “Metre Convention” (1875). Reúne-se em Paris a cada quatro ou seis anos.”
A unidade primária de medida de comprimento é o metro; no entanto, em algumas situações, essa unidade pode se tornar impraticável. Por exemplo, quando a medição envolve uma extensão muito grande, o metro pode ser considerado muito pequeno para essa finalidade. Por outro lado, em medições que envolvem extensões muito pequenas, o metro pode ser considerado excessivamente grande. Para contornar esse problema, o sistema métrico utiliza múltiplos e submúltiplos do metro.
| Nomes | Símbolos | Valores | |
|---|---|---|---|
| Múltiplos | Quilômetro |
km | 1000 m |
| Hectômetro | hm | 100 m | |
| Decâmetro | dam | 10 m | |
| Unidade | Metro | m | 1 m |
| Submúltiplos |
Decímetro | dm | 0,1 m |
| Centímetro | cm | 0,01 m | |
| Milímetro | mm | 0,001 m |
Além das unidades de medidas oficiais apresentadas, cabe mostrarmos outras unidades mais antigas, a exemplo:
| Polegada (Inglesa) | = | = | 2,54 cm | |
|---|---|---|---|---|
| Polegada (Portuguesa) | = | = | 2,75 cm | |
| Palmo | = | 8 polegadas | = | 22 cm |
| Pé | = | 12 polegadas | = | 33 cm |
| Vara | = | 5 palmos | = | 1,1 cm |
| Braça | = | 2 varas | = | 2,2 m |
| Légua de sesmaria ou brasileira | = | 3000 braças | = | 6600 m |
| Légua geométrica | = | = | 6000 m | |
| Milha brasileira | = | 1000 braças | = | 2200 m |
| Milha marítima | = | 1' de arco de meridiano * | = | 1852 m |
Exemplo 001: Converta para metros os seguintes valores:
a) 15.000 mm
b) 120 dam
c) 0,01 km
d) 1283 cm
e) 17 hm
f) 120 dm
g) 1.550.055 mm
h) 3.871 cm
i) 210 dam
j) 201 dm
3.1 Tipos de medidas lineares
As medidas lineares podem ser de três tipos.
DV = Distância Vertical
DI = Distância Inclinada
3.1.1 Horizontais
Referem-se às distâncias medidas em paralelo a um plano horizontal de referência. Essas medidas são utilizadas em Levantamentos Topográficos Planimétricos.
3.1.2 Verticais
Representam as distâncias medidas perpendicularmente a um plano horizontal de referência. Essas medidas são empregadas para quantificar as diferenças de altitude entre elementos da superfície e são fundamentais em Levantamentos Topográficos Altimétricos ou Planialtimétricos.
3.1.3 Inclinadas
Refere-se à medida de distância entre dois pontos em planos que seguem a inclinação da superfície do terreno.
3.2 Equipamentos de medição linear
3.2.1 Trena
É possível realizar medições em todas as direções. O material do qual pode ser composta a haste de medição inclui opções como fibra de vidro, aço com correção de temperatura (recomendada) e ínvar, que é a opção ideal.
3.2.2 Mira (regua graduada)
Instrumento auxiliar empregado para determinar distâncias horizontais e verticais com o auxílio de um teodolito.
3.2.3 Distanciômetro
É um dispositivo eletrônico que utiliza tecnologia a laser (Light Amplification by Stimulated Emission of Radiation) ou infravermelho para medir distâncias entre o equipamento e uma superfície refletora, frequentemente utilizando um prisma como alvo de reflexão.
3.2.4 Estação Total (teodolito + distanciômetro)
Da mesma forma que o distanciômetro, a Estação Total é um dispositivo eletrônico que usa tecnologia a laser ou infravermelho para medir distâncias entre o equipamento e uma superfície refletora, frequentemente um prisma. Além disso, a estação total também é capaz de medir ângulos.
4. MEDIDAS ANGULARES
Medidas angulares podem ser realizadas nos planos horizontal (o horizonte do instrumento) e vertical (o plano que contém a linha vertical do local). Dessa forma, temos os ângulos horizontais e verticais (Veras, 2012).
Quando se trata de medições angulares em um plano bidimensional, o Sistema Internacional (SI) define três unidades de medida: grau, grado e radiano (Silva; Segantine, 2015).
Os instrumentos topográficos para medição de ângulos frequentemente utilizam como unidade de medida o grau ou o grado.
4.1 Grau
A unidade de medida conhecida como grau é uma unidade sexagesimal na qual a circunferência é dividida em 360 partes iguais, sendo cada uma dessas partes equivalente a um ângulo de 1 grau (1°). Cada grau, por sua vez, é subdividido em 60 partes iguais, e cada uma dessas partes corresponde a um ângulo de 1 minuto (1'). Cada minuto é então subdividido em 60 partes iguais, com cada uma delas representando um ângulo de 1 segundo (1”) (Silva; Segantine, 2015).
O valor de 1 grau é igual ao ângulo central que intercepta, em uma circunferência, um arco cujo comprimento corresponde a 1/360 do comprimento total da circunferência.
Na unidade sexagesimal de graus, os graus, minutos e segundos são representados pelo símbolo de grau para os graus, um acento agudo para os minutos e aspas para os segundos. Esses símbolos são colocados na parte superior direita dos números correspondentes (Silva; Segantine, 2015). Dessa forma:
Lê-se: 175 graus, 23 minutos e 44 segundos.
O grau também pode ser representado usando uma segunda notação, chamada de notação decimal. Nessa forma numérica, estamos mais familiarizados, e o grau pode ser expresso como um número não inteiro. Por exemplo, o valor 175,3955556° (como mencionado anteriormente) pode ser simplificado para um único número decimal.
É viável converter valores entre as notações de grau decimal e sexagesimal. A notação decimal pode ser facilmente obtida a partir da notação sexagesimal usando a seguinte fórmula:
Exemplo 002: Converta para graus decimais, os seguintes ângulos em graus sexagesimais:
a) 75°15’25”
b) 23°37’42”
c) 36°61’12”
d) 90°45’22,5”
e) 47°17'18"
f) 143°53’59”
g) 180°59’61”
h) 235°28’36”
i) 301°00”58”
j) 359°59’59”
Assim como é possível realizar a transformação de graus sexagesimais em graus decimais, o caminho inverso é dado pela seguinte formulação:
Exemplo 003: Converta para graus sexagesimais, os seguinte ângulo em graus decimais: 75,789532158°
Grau = 75°
Minutos = (75,789532158 - 75) * 60 = 47,37192948 ⇒ somente a parte inteira ⇒ 47'
Segundos = (47,37192948 - 47) * 60 = 22,31576880"
R. 75°47'22,32"
Exemplo 004: Converta para graus sexagesimais, os seguintes ângulos em graus decimais:
a) 181,660833333
b) 72,460000000
c) 15,236944444
d) 100,000277778
e) 359,033055556
f) 2,666388889
g) 63,755000000
h) 54,528888889
i) 48,373611111
j) 276,153055556
4.1.1 Equipamentos de medição angular
4.1.1.1 Teodolito
Um dispositivo empregado para medir com precisão ângulos tanto horizontais quanto verticais é conhecido como teodolito. Embora os teodolitos atuais sejam todos eletrônicos, ainda é comum o uso de teodolitos óptico-mecânicos.
4.1.1.2 Estação Total
Assim como o teodolito, a estação total é capaz de medir ângulos tanto horizontais quanto verticais. A principal distinção entre elas e os teodolitos é que as estações totais também são capazes de medir distâncias. Importante notar que todas as estações totais são dispositivos eletrônicos e têm a capacidade de armazenar automaticamente as informações coletadas.
4.2 Grado
O valor de 1 grado corresponde ao ângulo central que intercepta um arco em uma circunferência, com um comprimento igual a 1/400 do comprimento total da circunferência.
Nesse contexto, a circunferência é dividida em 400 partes iguais, conforme ilustrado na figura, onde cada uma dessas partes representa um ângulo de 1g (um grado). Cada grado é subdividido em 100 partes iguais, com cada parte correspondendo a um ângulo de 1 centígrado ou 1 minuto centesimal. Além disso, cada centígrado ou minuto centesimal é subdividido em 100 partes iguais, onde cada uma delas equivale a um ângulo de 1 miligrado ou 1 segundo centesimal (Silva, Segantine, 2015).
Assim, 135,6342g corresponde a 135 grados, 63 centígrados e 42 miligrados ou 63 minutos centesimais e 42 segundos centesimais.
4.3 Relação entre grau e grado
A relação entre a medida de um ângulo em graus (°) e a mesma medida em grados (g) é determinada pela diferença entre as duas divisões, que são 360 e 400 partes (Veras, 2012). Portanto:
Exemplo 005: (Veras, 2012) Expressar no sistema sexagesimal o ângulo:
φ = 366g25′36"
φ° = (9/10)*366,2536g = 329°37'41,6"
Exemplo 006: Expressar no sistema sexagesimal o ângulo: φ = 283g37′10"
Exemplo 007: (Veras, 2012) Expressar no sistema centesimal o ângulo: φ = 165°15'40"
φg = (10/9)*165,2611111° = 183,6234568g = 183g62'34,568"
Exemplo 008: Expressar no sistema centesimal o ângulo: φ = 195°45'41"
4.4 Radianos
O valor de 1 radiano corresponde ao ângulo central que intercepta um arco de comprimento igual ao raio, quando consideramos uma circunferência com raio de 1 metro. Em outras palavras, um radiano é o ângulo central que corresponde a um arco de comprimento igual ao raio da circunferência.
Conforme ilustrado na figura abaixo, uma circunferência completa equivale a um ângulo de 2π radianos (6,283185 radianos), e um radiano corresponde a um ângulo de 57 graus, 17 minutos e 44,81 segundos. O ângulo reto, por sua vez, equivale a π/2 radianos. Devido ao fato de que o radiano expressa a relação entre dois comprimentos, ele é considerado uma unidade adimensional (Silva, Segantine, 2015).
4.5 Relação entre grau e radianos
Levando em consideração que o comprimento de uma circunferência com raio "r" é igual a 2πr, podemos estabelecer a seguinte relação:
Quando c = r ⟹ 1 radiano
α = 1rad = (180°)/π = 57°17'44,806"
Exemplo 009: (Veras, 2012) Expressar no sistema sexagesimal o ângulo: φ = 1,25614875rad
φ°=(180°)/π × 1,25614875 = 71°58'19,28"
Exemplo 010: Expressar no sistema radianos o ângulo: φ=257°00'15"
φrad = π/(180°) × 257°00′15" = 4,4855689
5 MEDIDAS SUPERFICIAIS
A unidade padrão para a medição de superfície no Sistema Internacional (SI) é o metro quadrado (m²). No entanto, em determinadas situações, é necessário utilizar múltiplos e submúltiplos dessa unidade.
| Nomes | Símbolos | Valores | |
|---|---|---|---|
| Múltiplos | Quilômetro Quadrado | km2 | 1 000 000 m2 |
| Hectômetro Quadrado | hm2 | 10 000 m2 | |
| Decâmetro Quadrado | dam2 | 100 m2 | |
| Unidade | Metro Quadrado | m2 | 1 m2 |
| Submúltiplos |
Decímetro Quadrado | dm2 | 0,01 m2 |
| Centímetro Quadrado | cm2 | 0,001 m2 | |
| Milímetro Quadrado | mm2 | 0,00001 m2 |
Nas medidas agrárias, é comum utilizar uma unidade denominada "are" (a). O are possui o hectare (ha) como seu múltiplo e o centiare (ca) como seu submúltiplo.
- 1 are (1 a) equivale a uma superfície de 10 m x 10 m = 100 m²
- 1 hectare (1 ha) equivale a uma superfície de 100 m x 100 m = 10.000 m²
- 1 centiare (1 ca) equivale a uma superfície de 1 m x 1m = 1 m²
Outras medidas usadas.
Fonte: Veras, 2012.
* Unidades muito usadas no Piauí nos processos de demarcação e divisão de Datas.
REFERÊNCIAS
CARDÃO, Celso. Topografia. Belo Horizonte: Ed. Arquitetura e Engenharia, 1970.
COMASTRI, J. A. Topografia Planimetria. Viçosa: IUUFV, 1977.
ESPARTEL, Lélis. Curso de Topografia. Rio Grande do Sul: Ed. Globo, 1980.
SILVA, I.; SEGANTINE, P. C. L. Topografia para engenharia: Teoria e prática de geomática. São Paulo: Ed. Elsevier, 2015.
VERAS, R. C. Notas de Aula. Teresina: UFPI, 2012.































0 comentários:
Postar um comentário